Regularization preserving localization of close edges
- The proposed approach is valid in the discrete domain as in the continous domain
- Close edges in image induce mutual influence in the detection process
- Mutual influence generaly leads to delocalization
- There are two types of configuration in mutual influence :
d is the distance between two close edges (d ≥ 1)
- To avoid delocalization of the edges, the regularization filter h must verifiy these conditions :
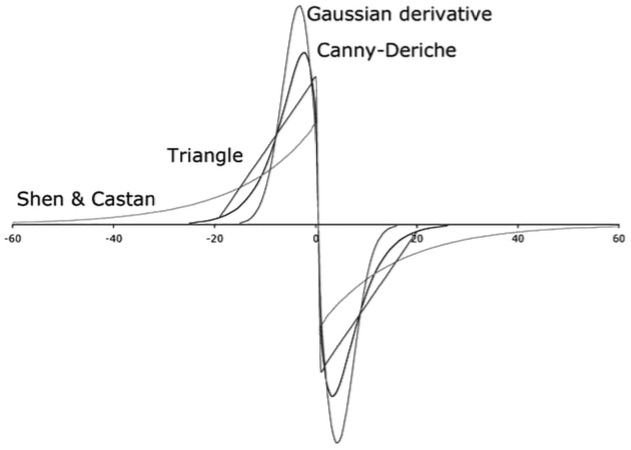
- Only one known detector verifies both these conditions
| filter h | delocalization in opposite configuration | delocalization in stair configuration |
| Canny or Gaussian derivative | Yes | Yes |
| Canny-Deriche | Yes | Yes |
| Shen & Castan | No | No |
| Demingy | Yes | No |
| Box | Yes | Yes |
| Triangle | Yes | No |
Example :
(Left) Original image. (Center) Detection by Shen and Castan filter . (Right) Detection by Gaussian (derivative) filter . Same SNR, Threshold . The last image presents clearly edge delocalization.
Conclusion: considering edge localization (with or without noise) gaussian filter is not a good candidate for regularization. Canny tried to take into account the problem of close edges in his work by introducing bounded filter support